Abstract
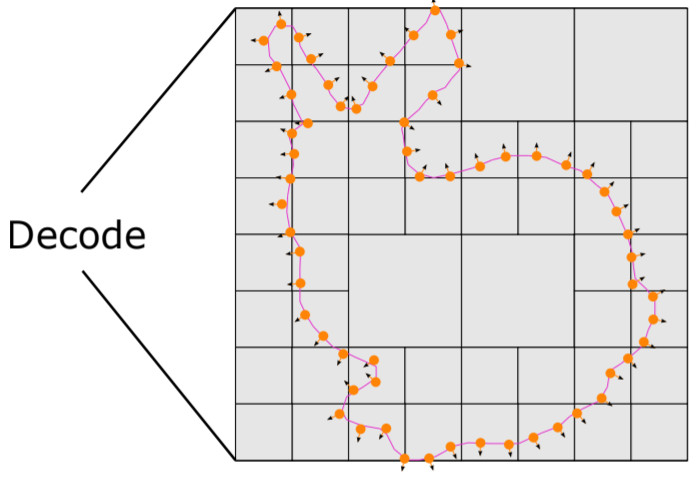
Point set is a flexible and lightweight representationwidely used for 3D deep learning. However, their discretenature prevents them from representing continuous and finegeometry, posing a major issue for learning-based shapegeneration. In this work, we turn the discrete point setsinto smooth surfaces by introducing the well-known implicitmoving least-squares (IMLS) surface formulation, which nat-urally defines locally implicit functions on point sets. Weincorporate IMLS surface generation into deep neural net-works for inheriting both the flexibility of point sets andthe high quality of implicit surfaces. Our IMLSNet pre-dicts an octree structure as a scaffold for generating MLSpoints where needed and characterizes shape geometry withlearned local priors. Furthermore, our implicit function eval-uation is independent of the neural network once the MLSpoints are predicted, thus enabling fast runtime evaluation.Our experiments on 3D object reconstruction demonstratethat IMLSNets outperform state-of-the-art learning-basedmethods in terms of reconstruction quality and computa-tional efficiency. Extensive ablation tests also validate ournetwork design and loss functions.